pressure in this space is figured by subtracting the
measured vacuum (10 in.Hg) from the nearly
perfect vacuum (29.92 in.Hg). The absolute
pressure then will be 19.92 or about 20 in.Hg
absolute. Note that the amount of pressure in a
space under vacuum can only be expressed in
terms of absolute pressure.
You may have noticed that sometimes we use
the letters psig to indicate gauge pressure and
other times we merely use psi. By common
convention, gauge pressure is always assumed
when pressure is given in pounds per square inch,
pounds per square foot, or similar units. The g
(for gauge) is added only when there is some
possibility of confusion. Absolute pressure, on the
other hand, is always expressed as pounds per
square inch absolute (psia), pounds per square
foot absolute (psfa), and so forth. It is always
necessary to establish clearly just what kind of
pressure we are talking about, unless this is very
clear from the nature of the discussion.
To this point, we have considered only the
most basic and most common units of measure-
ment. Remember that hundreds of other units can
be derived from these units; remember also that
specialized fields require specialized units of
measurement. Additional units of measurement
are introduced in appropriate places throughout
the remainder of this training manual. When you
have more complicated units of measurement, you
may find it helpful to review the basic informa-
tion given here first.
PRINCIPLES OF HYDRAULICS
The word hydraulics is derived from the Greek
word for water (hydor) plus the Greek word for
a reed instrument like an oboe (aulos). The term
hydraulics originally covered the study of the
physical behavior of water at rest and in motion.
However, the meaning of hydraulics has been
broadened to cover the physical behavior of all
liquids, including the oils that are used in modern
hydraulic systems. The foundation of modern
hydraulics began with the discovery of the
following law and principle:
. Pascal’s law—This law was discovered by
Blaise Pascal, a French philosopher and
mathematician who lived from 1623 to 1662 A.D.
His law, simply stated, is interpreted as pressure
exerted at any point upon an enclosed liquid is
transmitted undiminished in all directions.
Pascal’s law governs the BEHAVIOR of the static
factors concerning noncompressible fluids when
taken by themselves.
. Bernoulli’s principle—This principle was
discovered by Jacques (or Jakob) Bernoulli, a
Swiss philosopher and mathematician who lived
from 1654 to 1705 A.D. He worked extensively
with hydraulics and the pressure-temperature
relationship. Bernoulli’s principle governs the
RELATIONSHIP of the static and dynamic
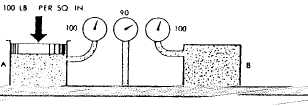
factors concerning noncompressible fluids. Figure
2-13 shows the effect of Bernoulli’s principle.
Chamber A is under pressure and is connected by
a tube to chamber B, also under pressure.
Chamber A is under static pressure of 100
psi. The pressure at some point, X, along the
connecting tube consists of a velocity pressure of
10 psi. This is exerted in a direction parallel to
the line of flow, Added is the unused static
pressure of 90 psi, which obeys Pascal’s law and
operates equally in all directions. As the fluid
enters chamber B from the constricted space, it
slows down. In so doing, its velocity head is
changed back to pressure head. The force required
to absorb the fluid’s inertia equals the force
required to start the fluid moving originally.
Therefore, the static pressure in chamber B is
again equal to that in chamber A. It was lower
at intermediate point X.
Figure 2-13 disregards friction, and it is not
encountered in actual practice. Force or head is
also required to overcome friction. But, unlike
inertia effect, this force cannot be recovered again
although the energy represented still exists
somewhere as heat. Therefore, in an actual system
the pressure in chamber B would be less than in
chamber A. This is a result of the pressure used
in overcoming friction along the way.
At all points in a system, the static pressure
is always the original static pressure LESS any
velocity head at the point in question. It is also
Figure 2-13.—Relationship of static and dynamic factors—
Bernoulli’s principle.
2-17